几个智能合约漏洞分析

二叉搜索树和红黑树简介

• 二叉搜索树：

二叉搜索树是一种节点值之间具有一定数量级次序的二叉树
对于树中的每个节点：如果存在左子树，则左子树的值小于根节点的值
如果存在右子树，则右子树的值一定大于根节点的值

• 红黑树：自平衡的二叉搜索树。

性质

性质1：每个节点要么是黑色，要么是红色。 
性质2：根节点是黑色。 
性质3：每个叶子节点（NIL）是黑色。 
性质4：每个红色结点的两个子结点一定都是黑色。 
性质5：任意一结点到每个叶子结点的路径都包含数量相同的黑结点。

红黑树的自平衡

• 自平衡的三种操作：左旋、右旋和变色
• 左旋：以某个结点作为支点（旋转结点），其右子结点变为旋转结点的父结点，右子结点的左子结点变为旋转结点的右子节点，左子结点不变。
• 右旋：以某个结点作为支点（旋转结点），其左子结点变为旋转结点的父结点，左子结点的右子结点变为旋转结点的左子结点，右子结点保持不变。
• 变色：结点颜色由红变黑或者由黑变红。

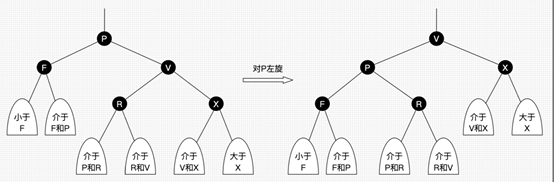
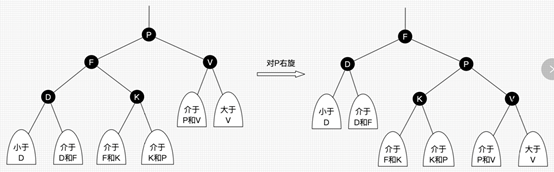
• 红黑树左旋/右旋的实际操作意义：

<1> 左旋只影响旋转结点和其右子树的结构，把右子树的结点往左子树挪。
<2> 右旋只影响旋转结点和其左子树的结构，把左子树的结点往右子树挪。
<3> 所以旋转操作是局部的。旋转保持红黑树平衡的端详：当一边子树的结点少了，那么向另外一边子树“借”一	些结点；当一边的子树的结点多了，那么向另外一边子树“租”一些结点。

红黑树的查找

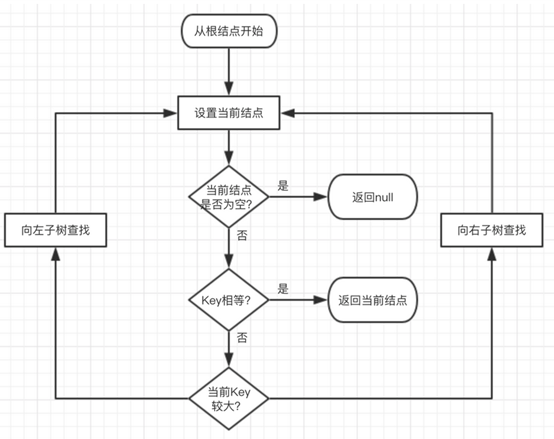
• 因为红黑树是一颗二叉平衡树，并且查找并不会破坏树的平衡，所以查找和二叉平衡树的查找无异。

1、从根节点开始查找，把根节点设置为当前结点；
2、若当前结点为空，返回NULL；
3、若当前结点不为空，用当前结点的key跟查找key作比较；
4、若当前结点key等于查找key，那么该key就是查找目标，返回当前结点； 
5、若当前结点key大于查找key，把当前结点的左子结点设置为当前结点，重复步骤2； 
6、若当前结点key小于查找key，把当前结点的右子结点设置为当前结点，重复步骤2；

红黑树的删除

• 删除时先作为普通二叉树进行删除：

1、若删除结点无子结点，直接删除。
2、若删除结点只有一个子结点，用子结点替换删除结点。
3、若删除结点有两个子结点，用后继结点（大于删除结点的最小结点）替换删除结点。（回到1和2）

• 寻找前继结点和后继结点的方法：将二叉树所有结点投射到X轴上，所有结点都是从左到右排序的，所有目标结点的前后结点就是对应前继和后继结点。

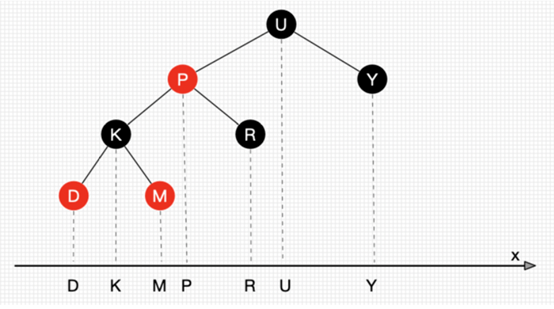
• 我们在删除红黑树结点时是先将他作为普通的二叉搜索树进行操作的，我们将结点删除后，再进行变色，避免同时操作时发生混乱。

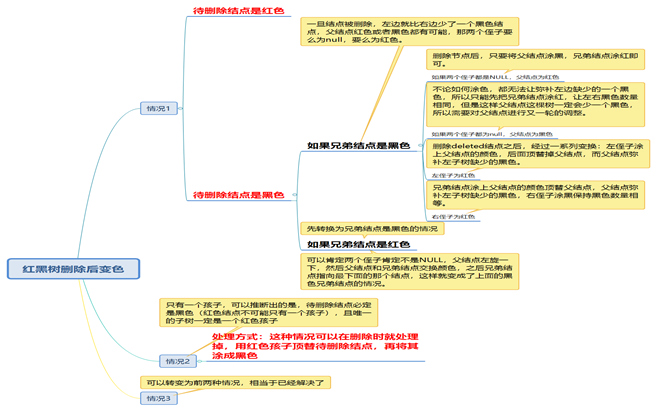
• 在删除结点时，我们可以将单一的结点树进行操作，而将未进行操作的树保留在一旁；整个的删除过程全部满足红黑树本身的五条性质，也就是说在变换过程中，对红黑树的一切操作都是为了让整个红黑树删除结点后依旧满足红黑树的性质。

---

转载请注明来源，欢迎对文章中的引用来源进行考证，欢迎指出任何有错误或不够清晰的表达。可以在下面评论区评论，也可以邮件至 1259742453@qq.com